接地BOX
"Plasma Simulations by Example"一书的学习笔记。
简介
模拟描述:等离子体被限制在一个接地的box内部,该Box接地且壁具有反射性。模拟运用静电PIC方法,并且是全动力学的。 这意味着离子和电子都被当作粒子来处理。虽然该模拟并没有那么令人兴奋,但它实际上会导致有趣的振荡现象。 还能够构建后续所有代码使用的基础框架。
模拟设置
模拟区域如下图所示:边长为0.2 m的立方体盒子,其空间范围从(-0.1, -0.1, 0)延伸到(0.1, 0.1, 0.2)。 区域被划分为一个\(21\times 21\times 21\)的均匀笛卡尔网格。模拟区域中初始均匀离子密度\(n_i = 10^11 m^{-3}\)。 电子密度与离子相同,但电子只占据\([-0.1,0)\times[-0.1,0)\times[0,0.1)\),也就是说: \[\begin{equation} n_e(\vec{x})=\left\{\begin{array}{ll}n_i&\quad;\vec{x}\in[\vec{x}_0,\vec{x}_c)\\0&\quad;\mathrm{otherwise}\end{array}\right. \end{equation}\]
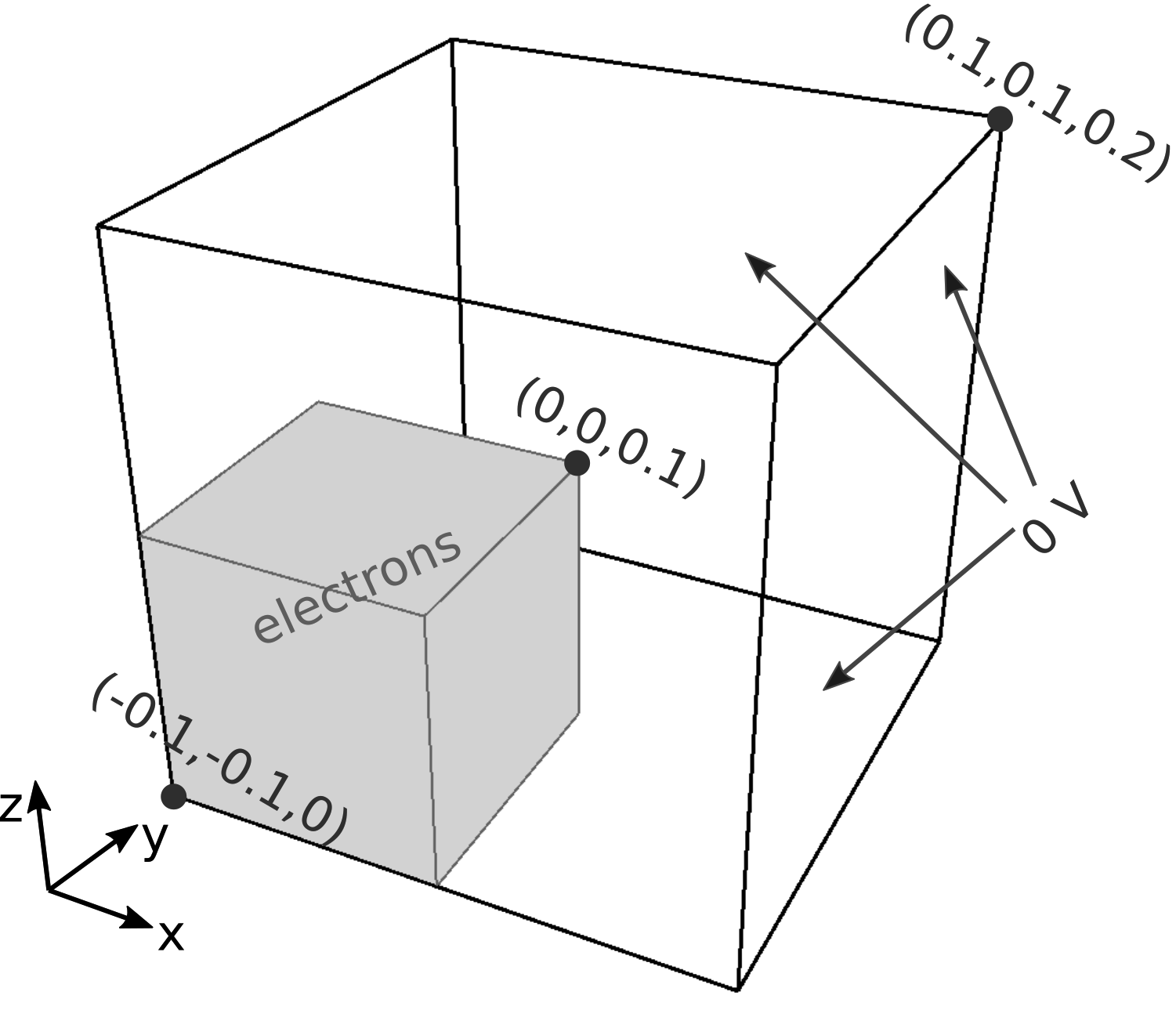
这个区域在图中用灰色框表示。这种设定明显是不稳定的。剩下的七个八分之一区域充满了净正电荷。可以预料,电子会试图进入这些区域以减少局部电荷分离。在这样做的过程中,它们会overshoot离子。在无限广阔的领域中,电子最终会返回,因为它们被困在一个类似于《等离子体模拟基础》所研究的势阱中。我们通过使壁具有反射性来近似这种行为。 0 V的Dirichlet边界条件被设定在所有边界上。
赝代码
代码是分块编写的。作者喜欢从一个仅有基本框架的应用程序开始,
这个框架包含了稍后要实现的功能hook。然后这些hook会逐一得到充实。初始的代码可能类似于如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27int main(int argc, char *args[]){
World world (/∗ . . . ∗/); // 初始化计算域
Species ions (/*...*/ ); // 初始化离子secies
Species electrons (/*...*/ ); // 初始化电子secies
SolvePotential(); // 得到初始化的电势
ComputeElectricField(); // 差分电势
GenerateParticles(); // 生成初始粒子
// 主循环
for (ts=0; ts<num_ts; ts++){
ComputeChargeDensity(); // 计算电荷密度
SolvePotential(); // 求解电势
ComputeElectricField(); // 计算电场
IntegrateVelocity(); // 更新粒子速度
IntegratePosition(); // 更新粒子位置
RunTimeDiagnostics(); // 输出一些诊断信息
}
OutputResults(); // 输出结果
return 0; // normal exit
}
我们首先定义一个名为World的变量,它封装了关于计算域的信息。接着,我们创建对象来存储离子和电子种类的数据。 这个对象属于Species类型,它存储了所有粒子共有的信息,比如它们的质量或电荷。 它还存储每个粒子的位置和速度。接下来,我们计算初始电场。这个电场对于Leapfrog方法中回溯粒子速度是必需的。 然后我们加载粒子。代码随后进入主循环。通常,我们会为预设的步数 num_ts 运行模拟。每一步都包括首先更新粒子的速度。 \[\begin{equation} \frac{d\vec{v}}{dt}=\frac qm\left(\vec{E}+\vec{v}\times\vec{B}\right) \end{equation}\] 在没有磁场的情况下,这会简化为: \[\begin{equation} \frac{d\vec{v}}{dt}=\frac qm\vec{E} \end{equation}\]
粒子的位置根据: \[\begin{equation} \frac{d\vec{x}}{dt}=\vec{v} \end{equation}\]
这些新位置随后被用来通过插值计算电荷密度\(\rho\),将其位置映射到网格上。然后求解泊松方程: \[\begin{equation} \nabla^2\phi=-\frac\rho{\epsilon_0} \end{equation}\]
电场是通过差分电势获得的: \[\begin{equation} \vec{E}=-\nabla\phi \end{equation}\]
最后,我们添加了一些屏幕和文件诊断工具,以揭示模拟的进展状况。就是这样!循环会持续迭代,直到达到所需的时间步数。
World对象
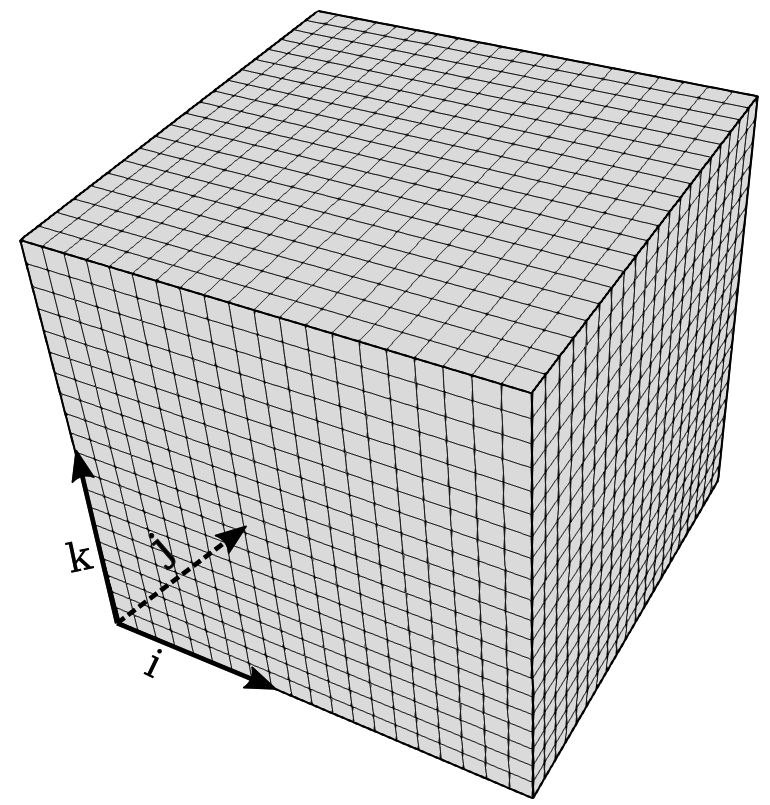
首先,需要建立一个用于存储网格几何形状和基于节点值的容器。这个例子中使用的笛卡尔网格如下图所示。 由于其规则的结构,只需要九个量就能完全描述这个网格:原点的三个浮点值\(x_0\)、\(y_0\)、\(z_0\);在\(x\)、\(y\)和\(z\)方向上的单元间距三个值:\(\Delta x\)、\(\Delta y\)和\(\Delta z\);以及节点计数\(ni\)、\(nj\)和\(nk\)。以向量形式表示为\(\vec{x}_0\)、\(\Delta\vec{h}\)以及\(\vec{nn}\)。这些信息被存储在一个名为World的对象中。一个简单的版本是:
1 | class World{ |
这种数据结构需要外部代码直接操作数组。例如, 1
2
3
4
5
6
7
8
9
10
11
12
13
14int main (){
World world;
world.nn[0] = 21; // 设置节点数
world.nn[1] = 21;
world.nn[2] = 21;
world.x0[0] = -0.1; // set origin
world.x0[1] = -0.1;
world.x0[2] = 0;
world.dh[0] = 0.01; // set mesh spacing
world.dh[1] = 0.01;
world.dh[2] = 0.01;
}
构造函数(constructor)
这种"C"风格的方法并不理想,因为它没有提供任何安全检查。
一旦相关数组初始化后,主函数中没有任何可以阻止修改变量(holding网格数量)的代码。这可能会导致内存损坏。C++提供了两种控制数据访问的工具。
首先,我们可以将类的成员定义为私有或受保护的,这阻止了类外部的任何代码访问它们。
或者,我们可以定义一个称为构造函数的特殊函数,每当对象初始化时都会自动调用。
它被定义为一个与类名相同且没有返回类型的函数。构造器使得我们可以初始化常量字段。这些成员可以在类外部读取,但一旦设置,它们的值就不能改变。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class World{
public:
World(int ni, int nj, int nk); // constructor
// 设置网格跨度,同时重新计算单元间距
void setExtents(double x1, double y1, double z1, double x2, double y2, double z2);
const int nn[3]; // 节点数量
const int ni, nj, nk; // number of nodes in individual variables
protected:
double x0[3]; // 网格原点
double dh[3]; // cell spacing in x, y, z
double xm[3]; // 网格最大值
double xc[3]; // 网格中心
};
protected 访问修饰符控制类成员的访问权限,位于 protected 下面的内容具有以下特性:
类内:可以在类的内部访问,如类的成员函数和友元函数。 派生类:可以在继承该类的派生类中访问。 外部访问:不能直接通过类的实例访问(与 private 类似)。
除了构造函数之外,我们还添加了一些额外的变量。其中包括“max
bound”,这是原点在对角线另一端相对应的点:\(\vec{x_m} = \vec{x_0} +\Delta \vec{h}\cdot
(\vec{nn}-1)\)。我们还添加了网格中心\(\vec{x_c}=(\vec{x_0}+\vec{x_m})/2\)。
非恒定数据被移动到一个受保护的区域,以防止外部访问。成员函数setExtents设置了网格的边界框,并且也计算了单元格的大小。主函数的调用现在如下所示。
1
2
3
4int main(){
World world(21, 21, 21);
world.setExtents(-0.1, -0.1, 0, 0.1, 0.1, 0.2);
}
声明与实现
至今我们只声明了类函数,但尚未实现它们。这可以通过在声明时提供函数体来完成,对于应该内联的小型函数来说,这确实是正确的选择。内联消除了与函数调用相关的开销。但是直接在类定义中包含代码有一些缺点。首先,或许算是一个小缺点,它会使代码更加杂乱。第二个原因与构建过程有关。C++通过三个步骤生成应用程序。首先,预处理器检查以#开头的特殊宏。其中一个,#include,允许我们导入另一个文件的内容。接下来,编译器生成实际的机器代码。为了调用函数或实例化类,编译器需要知道对象原型。原型告诉编译器函数期望的参数类型和返回类型是什么。 相似的信息由如上面所示的类声明提供。它允许编译器在实际上不知道成员函数具体做什么的情况下,构建和使用类型为World的对象。最后,链接器会查找函数体并确保它们在需要时可用。
多个文件
我们可以将程序拆分为多个文件,比如Main.cpp、Output.cpp、Solver.cpp、Species.cpp和World.cpp。这些文件随后可以通过构建过程包含进来:
1 | $ g++ -O2 Main.cpp Output.cpp Solver.cpp Species.cpp World.cpp -o ch2 |
-O2 是优化选项中的一个,表示中等程度优化。其作用是启用一系列优化,以提升生成的可执行程序的性能,而不会显著增加编译时间。在大多数情况下,这个优化级别可以显著提高程序性能,而且不会出现重大的代码错误或临时异常。详细来说,-O2启用的优化包括但不限于:
- 消除公共子表达式:检测和删除表达式中可以重复使用的部分,减少冗余计算。
- 删除死代码:去掉程序中不会被执行的代码。
- 代码内联:将小函数的代码直接插入调用处,以减少函数调用开销。
- 减少函数调用开销:通过转化一些递归为迭代、内联扩展等手段。
- 回合优化:多次遍历和优化代码的特定部分,以获取更高的性能提升。
如果所有的.cpp文件均在一个文件夹,则可写为: 1
g++ *.cpp -o ch2
1
$ g++ -c Main.cpp Output.cpp Solver.cpp Species.cpp World.cpp
1
$ g++ -c *.cpp
这个调用的输出则是五个对象文件:Main.o, Output.o, Solver.o, Species.o
和 World.o。然后我们将它们链接起来: 1
$ g++ Main.o Output.o Solver.o Species.o World.o -o ch2
假设我们只修改了在Main.cpp中定义的主要循环代码,其他四个文件无需重新编译。我们可以使用构建工具来重新构建这个应用:
1
2$ g++ -c Main.cpp
$ g++ *.o -o ch2
这虽然对于在这里开发的小型程序可能只是微不足道的时间节省,
但对于生产应用来说,有时从零开始编译可能需要花费数小时。make工具被用来通过自动确定哪些文件需要重新构建来自动化这一过程。
通过将函数体与其定义分离,我们减少了需要重新编译的代码量。我们在World.h头文件中编写World的定义,并在World.cpp源文件中包含适当的实现。其他需要使用World对象的文件则通过如下方法使用:
1
这些函数在World.cpp中的代码改变时无需重新编译。函数实现是通过在函数名称前加上类的名字来指定的。例如,
1
2
3void World::setExtents(double x1, double y1, double x2, double y2, double z2){
/*...*/
}
我们可能需要将函数定义与其实现分开的另一个原因是,假设我们有两个类A和B,每个类都需要调用另一个类的功能:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class B; // B是后面要定义的类
class A{
public:
void run(B &b){b.doSomething();}
void doSomething(){/*...*/}
};
class B{
public:
void run(A &a){a.doSomething();}
void doSomething(){/*...*/}
};
int main(){
A a;
B b;
a.run(b);
b.run(a);
return 0;
}
这段代码无法编译,因为当编译器运行A类中的(B
&b)函数时,它还不知道B类有一个名为doSomething()的成员方法。尽管在第1行使用前向声明(class
B)告知编译器B是一个类,但这种情况依然存在。交换类的顺序并无助于解决问题,因为两个类互相依赖。但通过将实现与定义分开,我们可以使代码成功编译。我们甚至不需要使用多个文件:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class B; // B是后面要定义的类
class A{
public:
void run(B &b){b.doSomething();}
void doSomething(){/*...*/}
};
class B{
public:
void run(A &a){a.doSomething();}
void doSomething(){/*...*/}
};
// 成员函数定义
void A::run(B &b){b.doSomething();}
void B::run(A &a){a.doSomething();}
int main(){
A a;
B b;
a.run(b);
b.run(a);
}
这个例子可能显得有些人为编造,但实际上在实践中确实会出现。在我们的例子中,创建物种对象时需要一个世界参照。然而,我们也在世界函数中使用物种来计算电荷密度。为了避免这种循环引用,这个函数的主体不得不被移出头文件。
头文件保护
最后,因为头文件可以包含其他头文件,有可能不经意间同一个文件被多次包含。这可能导致编译错误。为了防止这种情况,我们在头文件中使用头文件保护(header guard)来包裹内容。
1 |
|
这个构造利用预处理器来检查当前编译单元中是否已经定义了宏_WORLD_H。如果没有定义,我们就定义它,然后包含文件内容。否则,不包含任何内容。即使在打印的片段中未显示,这个构造也会用在所有示例的头文件中。
实施
考虑到这一点,我们继续实现World类。我们在World.cpp中添加以下代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20// Constructor
World::World(int ni, int nj, int nk) : ni{ni}, nj{nj}, nk{nk}, nn{ni, nj, nk}{}
// 设置网格扩展并计算单元格间距
void World::setExtents(double x1, double y1, double z1, double x2, double y2, double z2){
// 设置起点(xmin)
x0[0] = x1; x0[1] = y1; x0[2] = z1;
// 「对角线 - 反对角线 (xmax)」
xm[0] = x2; xm[1] = y2; xm[2] = z2;
// 通过将长度除以单元格数量计算间距
for (int i=0; i<3; i++){
dh[i] = (xm[i] - x0[i])/(nn[i]-1);
}
// 计算中心
for (int i=0; i<3; i++){
xc[i] = 0.5*(x0[i]+xm[i]);
}
}
构造函数通过初始化列表来设置类的常量成员。
大括号前的变量是类的成员,而里面的部分则是赋予它的值。
这些通常作为构造函数的参数。允许类成员和参数使用相同的名字。
然而,所有类都包含一个特殊的指针称为this,可以用来显式地引用类的成员。
通过这种方式使用this->ni=ni;可以作为将类成员设置为与局部变量(或函数参数)相同值的另一种方法,前提是这两个变量同名。
由于构造函数除了初始化数据之外没有其他操作,所以我们保持其body为空。
setExtents 函数首先为\(\vec{x}_0\) 和 \(\vec{x}_m\)向量设置值。这种初始化也可以作为构造函数的一部分,但是会导致函数参数过多。将调用分开使得代码更易于阅读,至少在我看来是这样。下一步,我们计算网格间距:
\[\begin{equation}
\Delta x=\frac{x_m-x_0}{n_i-1}
\end{equation}\]
这里,\(n_i\)表示沿x方向的节点数量,\(n_i - 1\)则是相应的单元格计数。 我们还设置了网格质心,\(\vec{x}c = (\vec{x}_m + \vec{x}_0)/2\)。质心仅仅用于加载电子群体。最后,我们调用一个函数来计算节点体积。这个函数尚未实现。
网格分辨率
在继续之前,我们应该指出cell间距不能完全随意设定。等离子体在比德拜长度更小的尺度上才不呈中性: \[\begin{equation} \lambda_D=\sqrt{\frac{\epsilon_0k_BT_e}{n_eq_e^2}} \end{equation}\] 其中,\(k_B\)是玻尔兹曼常量。该方程忽略了离子贡献,但由于\(T_i \ll T_e\),通常我们会忽略它。 既然我们关注的是模拟电子和离子的混合,就需要解决局部电荷分离的问题。 因此,我们需要cell体积小于德拜球的体积: \[\begin{equation} (\Delta x\Delta y\Delta z)<\frac43\pi\lambda_D^3 \end{equation}\] 或者,通常会要求: \[\begin{equation} \max(\Delta x,\Delta y,\Delta z)<\lambda_D \end{equation}\]
在我们的示例中,模拟前计算德拜长度并非易事,因为离子和电子都是冷加载的,\(T_e = T_i = 0\)。 然而,如后续章节(“结果”)所示,电子的总系统动能被限制在\(KE < 2\times 10^{-11}\) J。 考虑到该系统模拟了\(10^8\)个电子,我们可以计算出每个电子的动能为\(2\times 10^{-19}\) J。 对于麦克斯韦速度分布,我们也有\(KE = (3/2)kT\)。因此,如果我们假定电子是麦克斯韦分布的,$T_e $ K。 通常以电子伏特来表示温度,1 eV \(=(q/k_B)\approx 11604.5\) K。因此,$T_e = 0.83 $ eV。 再加上\(n_e = 10^{11}\),我们有\(\lambda_D = 0.0214\) m。对于\(20\times 20\times 20\)的网格, \(\Delta x=(x_m-x_0)/n_i=(0.2\text{m})/20=0.01\text{m}\) 我们的网格足够精细,能够解析德拜长度。如果有疑问,可以通过在不同网格分辨率下运行模拟并比较结果来进行网格收敛性研究。此外,根据我的经验,除非满足网格分辨率要求,否则高斯-赛德尔泊松求解器无法收敛。场求解器的发散是需要更细网格的一个好指示器。
场对象
我们现在已经完全定义了网格几何形状,但是这个网格中不包含任何数据。
在第一章中,我们使用了std::vector来存储一维数组,包含ni个条目。遗憾的是,C++标准库中并没有与之对应的三维容器,所以我们需要创建自己的数据结构。我们将这个对象称为Field。这一部分将详细讲述实现的细节。接下来的内容可能会稍显枯燥,所以你可以自由地跳过这一节。如果你选择跳过,只需了解Field存储三维双精度数据。我们还实现了FieldI,用于存储整数,以及Field3,用于存储三元向量。
沿着这条路,我们还定义了一个用于存储三元组浮点数和整型数的容器 double3
和 int3。 这些对象使用操作符重载来支持常见的数学运算。例如,不这样实现:
1
2
3double a[3], b[3], c[3];
for (int i=0; i<3; i++)
c[i] = a[3] + 5*b[i]; //在循环中计算每一个维度
我们可以简单写为: 1
2double3 a, b;
double3 c = a+5*b; // use overloaded * 以及 + 算符
同样地,我们可以在整个3D场中执行操作,例如: 1
2Field a, b;
Field c = a + 5*b; \\ every c[i][j][k] = a[i][j][k] + 5*b[i][j][k]
存储分配
C++
Field容器的主要目的是存储网格节点或cell中心数据。我们希望能够访问\(\phi\):
1 | Field phi(ni, nj, nk); // initialize memory for ni*nj*nk values |
C++与其他语言,如Java不同,它不原生支持多维数组的分配。这类数组通常是通过创建指针数组来近似的。
1 | double **v = new double*[5] |
分配一个包含五个双精度数据指针的数组。每个条目,比如v[3],是一个指针,可以指向任意的内存位置。
我们令: 1
v[3] = new double[10];
现在,v[3] 指向一个包含10个双精度浮点数的数组。我们通过 v[3][0] 到
v[3][9] 来访问这些值。
分配三维数据也类似。我们首先创建一个指向指针的数组。然后,每个条目被设置为指向一个指向双精度浮点数的指针数组,每个这样的指针又分配给一个双精度浮点数的数组。看起来是这样的:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28// Field.h
class Field{
pubic:
// constructor
Field (int ni, int nj, int nk) : ni{ni}, nj{nj}, nk{nk}{
data = new double**[ni]; // ni pointers to pointers
for (int i=0; i<ni; i++){
data[i] = new double*[nj]; // nj pointers to doubles
for (int j=0; j<nj; j++)
data[i][j] = new double [nk]; // nk double
}
}
// destructor,释放内存in reverse order
~Field(){
if (data==nullptr) return; // 返回如果分配了
for (int i=0;i<ni; i++){
for (int j=0; j<nj; j++){ // 释放内存in reverse order
delete data[i][j];
}
delete data[i];
}
delete[] data;
data = nullptr; // mark as free
}
const int ni, nj, nk; // number of nodes
protected:
double ***data;
};
析构函数是一种特殊函数,在对象的作用域结束时会自动调用。我们用它来释放内存。
1
2
3
4
5int main(){
Field phi(21, 21, 21); // calls Field constructor
/*...*/
return 0;
}// Field destructor called here automatically
python
对于python而言,内存管理由垃圾收集器处理,通常不需要手动释放内存。
1 | import numpy as np |
Julia
在 Julia
中,我们不需要显式地管理内存,垃圾收集器会自动处理内存释放。因此,不需要定义析构函数,类似
Python 的内存管理。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16module FieldModule
struct Field
ni::Int
nj::Int
nk::Int
data::Array{Float64,3}
# Construction function
function Field(ni::Int, nj::Int, nk::Int)
data = zeros(Float64, ni, nj, nk)
return new(ni, nj, nk, data)
end
end
end # modul1
2
3
4
5
6using .FieldModule
# 测试用例
field = FieldModule.Field(2, 3, 4)
println("数据内容:")
println(field.data)
Operator overloading
目前,没有直接访问存储在Field对象中的数据的方法。一种选择是将内部的double类型数据成员***data移动到公共区域。之后我们可以用phi.data[i][j][k]来访问数据。这种方式可能会比较繁琐。幸运的是,C++允许我们通过运算符重载定义自定义操作符。 几乎所有的运算符都可以重载,包括数组访问的方括号。
1 | class Field{ |
我们也可以重载赋值操作符,允许将所有字段条目设置为常量值。这在以下代码片段中展示:
1
2
3
4
5
6
7Field& operator=(double s){ // assignment operator
for (int i=0; i<ni; i++)
for (int j=0; j<nj; j++)
for (int k=0; k<nk;k++)
data[i][j][k] = s;
return *this; // 返回参照自身
}1
2
3Field phi(21, 21, 21);
phi = 0; // 初始化所有的值为0
phi[3][4][5] = 1.0; // 使用重载的操作符来设置数据1
2
3
4
5
6// constructor
Field (int ni, int nj, int nk): ni{ni}, nj{nj}, nk{nk}{
/* 内存分配代码来自上方 */
(*this) = 0; // 明确地使用赋值运算符
}1
2
3
4
5
6// 构造函数
Field (int ni, int nj, int nk) : ni{ni}, nj{nj}, nk{nk}{
/* 内存分配代码 */
operator = (0); // 调用重载操作符=为函数
}
模版
Field 对象目前被固定为处理双精度浮点数数据。
尽管在大多数情况下是如此,但有时我们需要存储不同类型的数据。这些包括用整数标记节点类型,以及用于表示速度和电磁场的(x,
y, z)向量。 C++ 允许我们使用模板将 Field
定义为一种通用容器。这个通用版本被重命名为 Field_,其内容如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36template <typename T>
class Field_{
public:
// 构造函数
Field_ (int ni, int nj, int nk): ni{ni}, nj{nj}, nk{nk}{
data = new T**[ni]; // ni pointers to pointers of type T
for (int i=0; i<ni; i++){
data[i] = new T*[nj]; // 分配指针nj到T
for (int j=0; j<nj; j++){
data[i][j] = new T[nk]; // 分配T类型的nk对象
}
}
(*this)=0; // clear data
}
// 析构函数
~Field_(){
/* 和之前的代码一样 */
}
// 数据访问操作
T** operator[] (int i) { return data[i];}
// overload赋值操作符
Field_<T>& operator= (T s){
for (int i=0; i<ni; i++)
for (int j=0; j<nj; j++)
for (int k=0; k<nk; k++)
data[i][j][k] = s;
return *this; // return reference to self
}
const int ni, nj,nk; // 节点数
protected:
T ***data; // pointer of type T
};1
2using Field = Field_<double>; // field of doubles
using FiedlI = Field_<int>; // field of integers
移动和复制构造函数
为了完整性,我们也应该定义两种特殊的构造函数,允许Field对象被复制和移动。第一种是拷贝构造函数,它通过逐个元素复制另一个Field对象来实现深拷贝。移动构造函数则“窃取”来自另一个对象的数据。它用于从函数中返回临时对象,否则这些对象需要被复制。这两种构造函数的代码如下。拷贝构造函数通过初始化列表调用标准构造函数来分配内存,然后逐个设置元素。
这一过程使用了重载的()运算符来读取另一个字段的数据。[]运算符支持对数据进行读/写访问,因为它返回对象的引用。它不适用于常量成员,因为可以通过引用改变值。()运算符通过返回存储的值提供只读访问数据的方式。而移动构造函数仅设置节点计数,并“窃取”数据,使我们的数据指针指向其他字段持有的数据。通过将其设置为nullptr,使其他字段的数据指针失效。
这阻止了析构函数尝试释放内存。赋值运算符也被重载以支持移动操作。&&
符号表示另一个是临时对象的引用。这些对象,也被称为
r-values,当从函数返回局部变量时会遇到。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Field{
// 复制构造函数
Field_(const Field_ &other):
Field_{other .ni, other .nj, other .nk}{
for (int i=0; i<ni; i++)
for (int j=0; j<nj; j++)
for (int k=0; k<nk; k++)
data[i][j][k] = other(i, j, k);
}
// 移动构造函数
Field_(Field_ &&other):
ni{other.ni}, nj{other.nj}, nk{other.nk}{
if (data) ~Field_(); // 处理分配数据
data = other.data; // 拿取数据
other.data = nullptr; // 无效化
}
// 移动标记操作
Field_& operator = (Field_ &&f){
if (data) ~Field_(); // 释放数据
data = f.data;
f.data=nullptr;
return *this;
}
// 只读访问数据 data[i][j][k]
operator() (int i, int j, int k) const {return data[i][j][k];}
};
Additional Operators
我们现在定义一些后续会派上用场的额外函数。首先是一个元素级除法运算符,
我们同样为复合加法定义了一个类似的运算符。
接下来,我们编写两个运算符,用于按标量缩放场。
代码的Python实现:step1
1 | #### World类 |
1 | #### 主代码 |
输出
Three-Component Vectors
向World中添加场
初始化输出
1 |
|
可视化
就目前而言,我可能更关切的是用Python实现,暂时还不考虑性能问题。因此上述部分C++代码讲解跳过。
代码的Python实现:step2
World 类
1 | import numpy as np |
Output类
1 | import io |
主代码
1 | import sys |
势求解器
上一章节介绍了Gauss-Seidel 算法求解泊松方程。我们从离散化控制方程开始: \[\begin{equation} \nabla^2\phi=-\rho/\epsilon_0 \end{equation}\]
\[\begin{equation} \begin{aligned}\frac{\phi_{i-1,j,k}-2\phi_{i,j,k}+\phi_{i+1,j,k}}{\Delta^2x}+\frac{\phi_{i,j-1,k}-2\phi_{i,j,k}+\phi_{i,j+1,k}}{\Delta^2y}+\\\frac{\phi_{i,j,k-1}-2\phi_{i,j,k}+\phi_{i,j,k+1}}{\Delta^2z}&=-\rho_i/\epsilon_0\end{aligned} \end{equation}\]
离散基于二阶中心差分。\(\Delta^2x=(\Delta x)^2\)。接下来将所有\(\phi_{i,j,k}\)项都放在等式左侧: \[\begin{equation} \begin{aligned}\left(\frac{2}{\Delta^2x}+\frac{2}{\Delta^2y}+\frac{2}{\Delta^2z}\right)\phi_{i,j,k}=\rho_i/\epsilon_0+\frac{\phi_{i-1,j,k}+\phi_{i+1,j,k}}{\Delta^2x}+\\\frac{\phi_{i,j-1,k}+\phi_{i,j+1,k}}{\Delta^2y}+\frac{\phi_{i,j,k-1}+\phi_{i,j,k+1}}{\Delta^2z}\end{aligned} \end{equation}\]
最后,为了求解\(\phi_{i,j,k}\),我们得到一个关于节点i、j、k处电势新估计的方程。 高斯-塞德尔常与连续过松弛法(SOR)结合使用,以加速收敛。最终的方程为 \[\begin{equation} \begin{aligned}\phi_{i,j,k}^*=\left(\rho_i/\epsilon_0+\frac{\phi_{i-1,j,k}+\phi_{i+1,j,k}}{\Delta^2x}+\frac{\phi_{i,j-1,k}+\phi_{i,j+1,k}}{\Delta^2y}+\right.\\\frac{\phi_{i,j,k-1}+\phi_{i,j,k+1}}{\Delta^2z})/\left(\frac{2}{\Delta^2x}+\frac{2}{\Delta^2y}+\frac{2}{\Delta^2z}\right)\end{aligned} \end{equation}\] 以及 \[\begin{equation} \phi_{i,j,k}\leftarrow\phi_{i,j,k}+w(\phi_{i,j,k}^*-\phi_{i,j,k}) \end{equation}\] 此处,箭头表明了我们将右侧的值 overwriting \(\phi_{i,j,k}\)的值。上述算法仅在内部节点(中心差分可以被 evaluated)上有效。一般情况下,我们需要添加方程以控制边界。由于此处box walls被假定为Dirichlet,我们通过将循环限制在内部网格节点上(\(i\in[1,ni-2]\)、\(j\in[1,nj-2]\)以及\(k\in[1,nk-2]\))以简单的跳过它们(边界?)。求解器被定义为位于 PotentialSolver.h 中的PotentialSolver对象的成员函数。
1 | class PotentialSolver{ |
构造函数接受一个对World对象的引用作为参数,我们将其保存为类成员。 这个引用是为了访问phi场和网格几何结构。我们还设置了一些求解器参数:最大迭代次数和容差。实际的高斯-赛德尔算法在PotentialSolver.cpp中的solve函数中实现。
1 | bool PotentialSolver::solve(){ |
我们首先建立对phi和rho的local引用。这一步骤是为了美观,避免每次我们需要访问势能时都必须写出world.phi。 每隔25次迭代,计算残差向量: \[\begin{equation} \vec{R}=\mathbf{A}\vec{x}-\vec{b} \end{equation}\]
并比较L2范数 \[\begin{equation} \sqrt{\frac{\sum_nR_n^2}n}\leq\epsilon_{tol} \end{equation}\] 达到某种tolerance。这种收敛检查会跳过边界,因为那里自然满足狄利克雷条件。如果求解器无法达到所需的容忍度,我们会打印错误信息并返回false,表示失败。然后,我们可以重新运行求解器,增加迭代限制次数,或者像我经常做的那样,如果只在最初的几次时间步长中出现非收敛消息时,直接忽略它。物理常数以及其他一些常数的值是通过在World.h中添加的命名空间Const提供的。
由于目前\(\rho\)为零(我们还没有添加任何粒子),上述代码会在所有位置产生\(\phi\)等于0的结果。
这并不十分有趣。仅仅为了确认求解器确实能运行,我们通过在主程序中添加以下技巧,让\(\phi_{i = 0} = 1\),\(\phi_{k = 0} = 2\)。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23int main(){
// 初始化domain
World world(21, 21, 21)
world.setExtents({-0.1, -0.1, 0.0},{0.1,0.1, 0.2});
// 设定phi[i=0]=1以测试
for (int j=0; j<world.nn[1]; j++)
for (int k=0; k<world.nn[2]; k++)
world.phi[0][j][k] = 1; // phi[i=0]
// 设定phi[k=0]=2以测试
for (int i=0; i<world.nn[0]; i++)
for (int j=0; j<world.nn[1]; j++)
world.phi[i][j][0] = 2; // phi[k=0] = 2
// 初始化和求解电势
PotentialSolver solver(world, 5000, 0);
solver.solve();
// 保存结果
Output::fields(world);
return 0;
}
电场
在ES-PIC模拟中,等离子体势仅仅是一块垫脚石,用于获取电场: \[\begin{equation} \vec{E}=-\nabla\phi\equiv-\left(\frac{\partial\phi}{\partial x}\hat{i}+\frac{\partial\phi}{\partial y}\hat{j}+\frac{\partial\phi}{\partial z}\hat{k}\right) \end{equation}\] 我们仍使用有限差分方法来重写导数。根据中心差分,我们有: \[\begin{equation} \begin{aligned} \vec{E}=&\left(\frac{\phi_{i-1,j,k}-\phi_{i+1,j,k}}{2\Delta x}\right)\hat{i}+\left(\frac{\phi_{i,j-1,k}-\phi_{i,j+1,k}}{2\Delta y}\right)\hat{j}+\\&\left(\frac{\phi_{i,j,k-1}-\phi_{i,j,k+1}}{2\Delta z}\right)\hat{k} \end{aligned} \end{equation}\] 该差分只适用于内部节点。在边界上,我们使用前一章中研究的单侧二阶精度: \[\begin{equation} \begin{aligned} \left(E_x\right)_{i=0}& \large=\frac{3\phi_{0,j,k}+4\phi_{1,j,k}-\phi_{2,j,k}}{2\Delta x} \\ \left(E_x\right)_{\boldsymbol{i=}n\boldsymbol{i-1}}& =\frac{-\phi_{ni-3,j,k}+4\phi_{ni-2,j,k}-\phi_{ni-1,j,k}}{2\Delta x} \end{aligned} \end{equation}\]
在\(y\)和\(z\)面具有相似的方程。这些关系式在computeEF函数中实现。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39// 计算电场 = -梯度(phi)
void PotentialSolver::computeEF(){
// reference to phi以避免写world.phi
Field &phi = world.phi;
double3 dh = world.getDh
double dx = dh[0]
double dy = dh[1]
double dz = dh[2]
for (int i=1; i<world.ni; i++) // 对整个节点循环
for (int j=1; j<world.nj; j++)
for (int k=1; k<world.nk; k++){
double3 &ef = world.ef[i][j][k]; // ref to (i,j,k) ef vec3
// x component, efx
if (i==0) // 向前差分
ef[0] = -(-3*phi[i][j][k] + 4*phi[i+1][j][k] - phi[i+2][j][k])/(2*dx);
else if (i==world.ni-1) // 向后差分
ef[0] = -(phi[i-2][j][k] - 4*phi[i-1][j][k] + 3*phi[i][j][k])/(2*dx);
else // 中心差分
ef[0] = -(phi[i+1][j][k] - phi[i-1][j][k])/(2*dx);
// y component, efy
if (j==0)
ef[1] = -(-3*phi[i][j][k] + 4*phi[i][j+1][k] - phi[i][j+2][k])/(2*dy);
else if (j==world.nj-1)
ef[1] = -(phi[i][j-2][k] - 4*phi[i][j-1][k] + 3*phi[i][j][k])/(2*dy);
else
ef[1] = -(phi[i][j+1][k] - phi[i][j-1][k])/(2*dy);
// z component, efz
if (k==0)
ef[2] = -(-3*phi[i][j][k] + 4*phi[i][j][k+1] - phi[i][j][k+2])/(2*dz);
else if (k==world.nk-1)
ef[2] = -(phi[i][j][k-2] - 4*phi[i][j][k-1] + 3*phi[i][j][k])/(2*dz);
else
ef[2] = -(phi[i][j][k+1] - phi[i][j][k-1])/(2*dz);
}
}
粒子
下一步,我们需要写载入和移动粒子的代码。作者喜欢通过气体种类分类粒子。
它也简化了计算宏观流动性质的过程,比如粒子数密度和平均流速。我们首先定义一个新的数据容器来存储单个粒子。
1
2
3
4
5
6
7
8
9
10struct Particle{
double pos[3]; // 位置
double vel[3]; // 速度
double mpw; // 宏观粒子权重
Particle (double x[3], double v[3], double mpw): // 构造函数
pos{x[0],x[1],x[2]},
vel{v[0],v[1],v[2]},
mpw{mpw}{ }
};
这个物体存储了定义一个粒子所需的基本信息。具体来说,存储了粒子的位置\(\vec{x}\)和速度\(\vec{v}\)。 我们也存储宏粒子权重\(w_{mp}\)。多数情况下,所有粒子具有相同的权重,而\(w_{mp}\)可以delegated到species级别处理。 我们在这里保留它一般性。
下一步我们定义Species对象。构造函数接受一个字符串参数,表示物种的名称,每个粒子的质量和电荷,以及对World对象的引用。
这个对象用来初始化一个局部变量Field,用于存储数密度。我们还声明了几个稍后将实现的函数。
实际的粒子存储为一个名为particles的vector
1 | class Species{ |
离子和电子species通过实例化Species类型的变量以添加到模拟中。我们存储这些对象
within another vector。 该方法允许我们自动化后续的操作 that 包括循环整个
flying materials。
标准库vector中的向量支持自动调整大小。但是调整大小涉及到复制(或移动)之前存储的数据,因此,如果我们提前知道需要存储多少项,预先使用reserve命令分配足够的空间对我们有利:
1
2
3
4
5
6
7
8
9
10
int main(){
/* World初始化 ... */
// 设定粒子species
vector<Species> species;
species.reserve(2); // 预先分配两种物种的空间
species.push_back(Species("O+", 16*AMU, QE, world)); // AMU 单位原子质量
species.push_back(Species("e-", Me, -1*QE, world)); // 电子质量
}
载入粒子
随后通过加载粒子来初始化populations。我们感兴趣的是加载粒子以使得在特定bounding box中获得物种数密度。 对于离子,该bounding box的尺寸与计算域相同,而对于电子来说,它只包含选定的八分之一区域。 由于数密度是单位体积粒子数量,那么具有数密度\(n\)体积\(V\)的box中包含\(N_{real}=nV\)个物理离子或电子。 这个数量的真实粒子由\(N_{sim}\)个模拟宏粒子表示,因此每个粒子的权重为\(w_{mp} = N_{real}/N_{sim}\)。 此处, \(N_{sim}\) (或\(M\)使用我们之前语法)是用户输入的。 这个计算过程如下所示。一旦我们确定了权重,我们就使用循环来采样\(N_{sim}\)个粒子的位置和速度。这个采样的具体细节目前忽略不计。 在添加粒子之前,我们通过调用reserve预留足够空间来存放num_mp个粒子。这样可以避免当向量需要调整大小时,之前插入的数据需要移动或复制。
1 | void loadParticles(double3 x1, double3 x2, double num_den, int num_mp){ |
随机数
一种明显的采样位置方法是选择兴趣区域内的一个随机点。我们可以通过下面的方式来生成在\([x_1, x_2)\)范围内的随机数: \[\begin{equation} \begin{aligned}x=x_1+\mathcal{R}(x_2-x_1)\quad&\in[0,1)\end{aligned} \end{equation}\] 其中\(\mathcal{R}\)是随机数。随机数是通过称为随机数生成器或RNG的函数生成的。 重要的是要认识到,随机数生成器通常并不会生成真正的随机数。相反,它们会从一个足够长的序列中连续返回数值,这个序列长度使得对于一般观察者来说,这些数字看起来确实像是随机的。这个序列的长度——即在数字开始重复之前可以采样的唯一数值的数量——被称为周期。使用具有大周期的生成器是至关重要的。
1 | // World.h |
构造函数通过创建random_device对象的实例并从中采样一个值来设置初始seed。
如果我们想要使用相同的一组随机数重复模拟,我们将用mt_gen{0}(或者某个其他固定值)替换这种初始化方式。
然后,在World.cpp中,我们创建了一个名为rnd的Rnd类型的实例。
1
Rnd rnd; // 创建一个Rnd对象的实例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16void Species::loadPatticlesBox(double3 x1, double3 x2, double num_den, int num_mp){
/* same code as above */
// load particles on an 相等间距网格
for (int p=0; p<num_mp; p++){
// sample random position
double3 pos;
pos[0] = x1[0] + rnd()*(x2[0] - x1[0]);
pos[1] = x1[1] + rnd()*(x2[1] - x1[1]);
pos[2] = x1[2] + rnd()*(x2[2] - x1[2]);
// set initial velocity
double3 vel {0, 0, 0}; // 静止粒子
vel[0] = rnd()*v_max[0]; // 将一个新粒子添加到数组中
}
}addParticle
函数简单地向粒子向量中添加一个新的条目, 1
2
3void Species::addParticle(double3 pos, double3 vel, double3 mpw){
particles.emplace_back(pos, vel, mpw);
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17int main(){
/* ... */
// 设定粒子种类
vector<Species> species;
species.push_back(Species("O+", 16*AMU, QE, world));
species.push_back(Species("e-", ME, -1*QE, world));
int np_ions = 80000; // 模拟离子数量
int np_eles = 10000; // 模拟电子数量
species[0].loadParticlesBox(world.getX0(), world.getXm(), 1e11, np_ions); // 加载离子
species[1].loadParticlesBox(world.getX0(), world.getXc(), 1e11, np_eles); // 加载电子
// 使用范围样式循环打印粒子计数
for (Species &sp:species)
cout<<sp.name<<" has "<<sp.getNp()<<" particle"<<endl;
}1
2
3
4for (vector<Species>::iterator iter = species.begin(); iter!= species.end(); ++iter){
Species &sp = *iter; // 元素在当前迭代位置
/* use sp here */
}
此时,无法检查加载是否按预期进行。虽然我们可以在其中添加一个输出函数,生成粒子位置的散点图,但我们将此留到下一章。 相反,我们从粒子数据计算数密度。数密度是指在小区域内粒子的数量除以该区域的体积。单元大小控制着我们可以解析的空间细节程度。 由于我们感兴趣于计算节点中心的量,所以我们定义了一个以节点为中心的、大小与单元相等的控制体积。这意味着每个体积延伸至相邻单元的质心。
在一个笛卡尔网格中,每个单元体的体积为 \(V=\Delta x \Delta y \Delta z\)。节点的体积与cell相同,至少在远离边界的内部区域是这样。 在边界面,节点体积减半。这些节点索引要么是0,要么是ni-1, nj-1, nk-1。边上的节点,若其有两个零或ni - 1, nj - 1, 或nk - 1的索引,它们的体积会减少四分之一。最后,位于角落的节点体积会减少八分之一。换句话说,每增加一个边界索引,节点体积就减少二分之一。 这项计算由World类中的一个名为computeNodeVolumes的函数执行,每当世界范围发生变化时,它就会被调用。该函数的声明被添加到World类的受保护区块中。
1 | // 计算节点体积,在整数节点上dx*dy*dz |
在setExtents中call该函数: 1
2
3
4void World::setExtents(double3 _x0, double3 _xm){
/* ... */
computeNodeVolumes();
}
散射:粒子到网格插值
一种计算数密度的方法是统计每个控制体积内的粒子数量。这种零阶方法不被推荐,因为它不会导致粒子在cell间穿行时密度的平滑变化。 我们使用一种被称为scatter的方法,它是之前提的gather方法的反过程。它使我们能够将particle-based data内插到计算网格中。 数据scattered到八个(在三维中)节点上,这些节点构成包含粒子的cell。由于节点在单元之间共享,这种内插确保了周围单元也“感知”到粒子。
scatter算法的第一步是确定粒子属于哪一个cell。这对于笛卡尔坐标系来说非常简单,因为节点位置的方程可以解析地求逆。 我们有: \[\begin{equation} l_i=(x-x_0)/\Delta x\\ l_j=(y-y_0)/\Delta y\\ l_k=(z-z_0)/\Delta z \end{equation}\]
这些索引是浮点数。整数部分对应于节点索引,而小数部分则是相对于正i、j或k方向上相邻节点的归一化距离。 我们实现在一个名为XtoL的函数中进行这项计算。这个函数直接在World.h头文件中实现,以便编译器可以进行内联处理。我们还将该函数标记为const,以表明它不会修改类的数据。这个注解可以带来额外的优化。
1 | class World{ |
我们接着使用整数转换int(\(l_i\))来获取节点索引。使用粒子位置,cell
可以被划分为八个八分之一。
其normalized体积被用来确定粒子数据分配到每个8节点的比例。数据deposited在“对角线相对(diagonally-opposed)”方向。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22void Field::scatter(double3 lc, double value){
// 确保我们在domain内
if (lc[0]<0 || lc[0]>=nx-1 || lc[1]<0 || lc[1]>=ny-1 || lc[2]<0 || lc[2]>=nz-1) return; // 如果上述任一条件为真(即任一坐标超出边界),则执行 return,退出当前函数。这意味着代码不会继续执行后面的逻辑
// 计算cell索引和分数距离
int i = (int)lc[0];
int j = (int)lc[1];
int k = (int)lc[2];
double di = lc[0] - i;
double dj = lc[1] - j;
double dk = lc[2] - k;
// deposit 分数值到8个周围的节点
data[i][j][k] += (1-di)*(1-dj)*(1-dk)*value;
data[i+1][j][k] += di*(1-dj)*(1-dk)*value;
data[i+1][j+1][k] += di*dj*(1-dk)*value;
data[i][j+1][k] += (1-di)*dj*(1-dk)*value;
data[i][j][k+1] += (1-di)*(1-dj)*dk*value;
data[i+1][j][k+1] += di*(1-dj)*dk*value;
data[i+1][j+1][k+1] += di*dj*dk*value;
data[i][j+1][k+1] += (1-di)*dj*dk*value;
}
现在将computeNumberDensity函数添加到Species类中: 1
2
3
4
5
6
7
8void Species::computeNumberDensity(){
den = 0; // 设定所有值为零
for (Particle &part:particles){ // loop over particles
double3 lc = world.XtoL(part.pos); // 得到逻辑坐标
den.scatter(lc, part.mpwt); // deposit weight
}
den /= world.node_vol; // divide by node volume
}
这个函数首先通过使用2.4.2节中介绍的重载赋值运算符,将所有数值设为零,从而清空数据。 接着,我们遍历所有粒子。计算逻辑坐标,并利用它将宏粒子的质量分散到网格中。分散过程是累加的,因此在这一步之前需要清空场。 在粒子循环完成后,den 对象包含了被插值到网格节点上的真实粒子数量。但由于我们关心的是密度,我们需要将这些计数除以节点体积。 在这里,我们使用了重载的 /= 运算符。如果在不支持运算符重载的编程语言中开发代码(或者你只是不喜欢它们),你可以定义一个名为 divideByField 的函数来执行这种逐元素的除法操作。
我们还修改了Output::fields函数,使其接收第二个参数,即物种向量的reference。我们遍历成员,并将密度场作为名为nd.O+和nd.e-的数据数组输出。
1
2
3
4
5
6
7
8
9
10
11void Output::fields(World &world, vector<Species> &species){
/*...*/
// species数密度
for (Species &sp:species){
out<<"<DataArray Name=\"nd."<<sp.name<<"\"
NumberOfComponents = \"1\" format=\"ascii\"
type=\"Float64\">\n";
out<<sp.den;
out<<"</DataArray>\n";
}
}
电荷密度
有了粒子数密度,就可以计算电荷密度了。
